
在学习 Coursera.org 上 Model Thinking 课程过程中,觉得决策树Decision Tree 特别有趣,可以在日常生活中用以辅助个人的决策。人人都希望用理性指导自己的生活,实际上绝大部分一生中的绝大部分(包括最重要的)决策都是非理性的(至少我是这样)。
设想你在读大学,目前有一个申请奖学金的项目,程序如下:最多200名同学可以申请,申请者需提交2页的小论文一篇;评审会将200名申请者中,根据论文质量择优选择10名申请者入围最终评选。这10名入围者又需要各自提交一篇10页的论文。最终根据论文质量,在10名申请者中确定1名给与奖学金5000元。
很少有人想到,这个问题可以使用数学中概率的决策树来解决。
我们先确定成本:
- 假设2页的论文成本为:20元。
- 假设10页的论文成本为:40元。
我们再画出决策树:
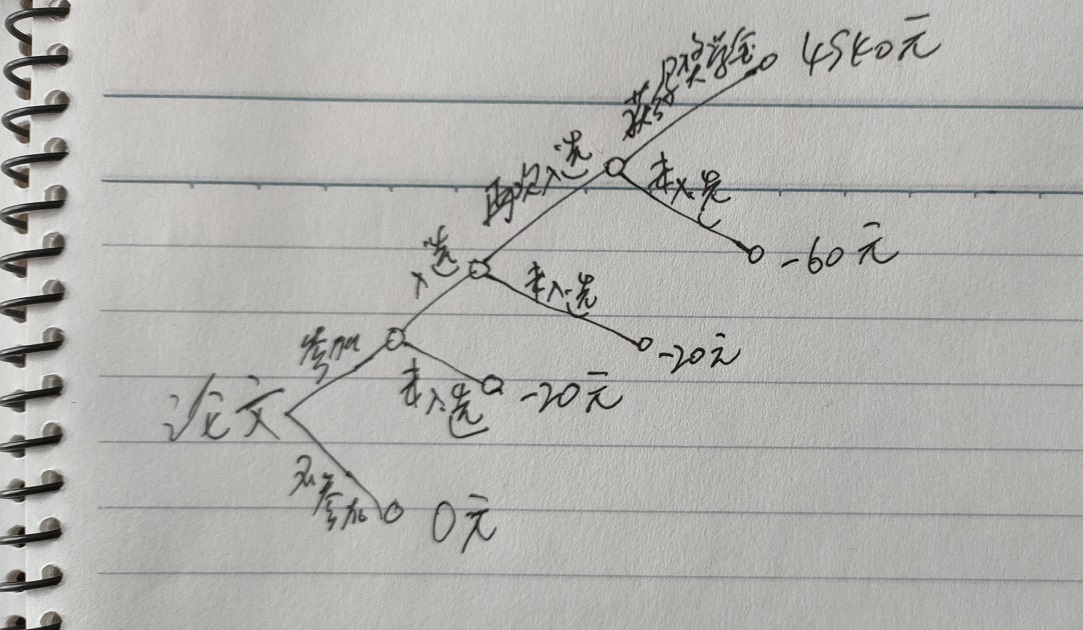
决策过程:
- 如果不参加申请,成本为0元
- 如果参加申请,此时是200名申请者选择10名,入选概率
10/200=0.05,被淘汰概率0.95- 如果被淘汰,损失
20元(2页论文成本) - 如果入选,再次提交10页论文,此时入选概率为
1/10=0.1,被淘汰概率0.9- 如果被淘汰,损失
60元(2页论文20元+10页论文40元) - 如果再次入选,获得
4940元(5000元奖学金-60元论文成本)
- 如果被淘汰,损失
- 如果被淘汰,损失
那么,申请还是不申请呢?咱们使用概率计算一下。在最终10选1的时候,
- 入选概率为
0.1,获益为4940元,期望收益4940✖0.1=494元 - 落选概率为
0.9,获益为-60元,期望收益-60✖0.9=-54元
在第二轮的期望收益为:494-54=440元。第一轮200选10的时候,
- 入选概率为
0.05,获益440元,期望收益440✖0.05=22元 - 落选概率为
0.95,获益-20元,期望收益-20✖0.95=-19元
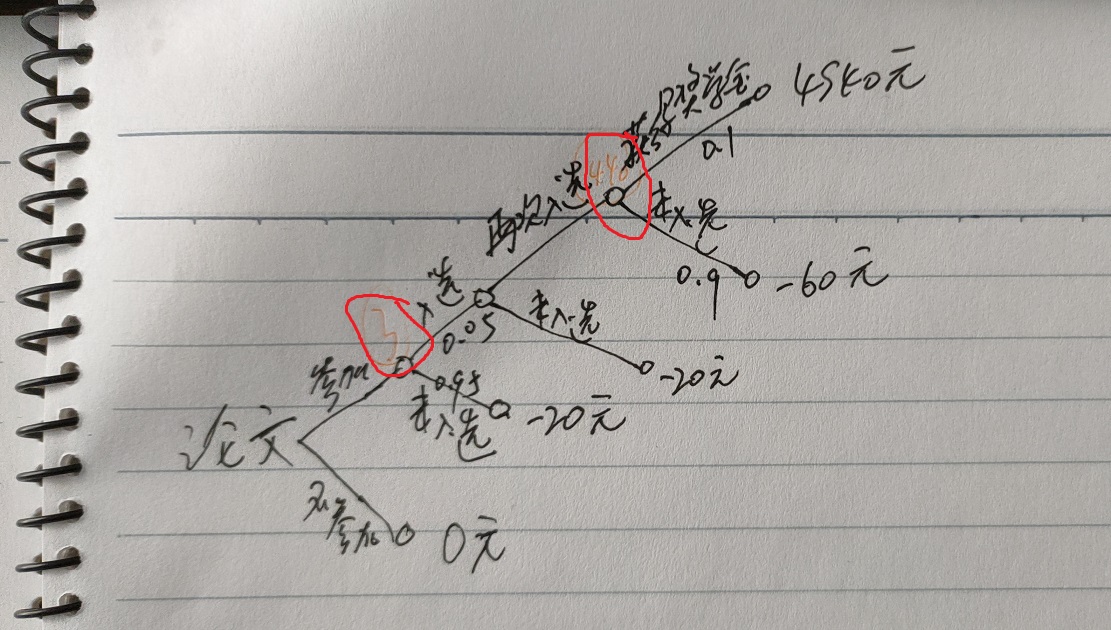
22-19=3元,如果不参加申请成本为0元,3>0,结论是我们应该参加申请。
拓展题:初选阶段如果不是200名而是300名同学申请,还有必要参加吗?