第二十一章《根据t分布进行区间估计——未知总体方差时以正态母群体推算总体均值》。
总结
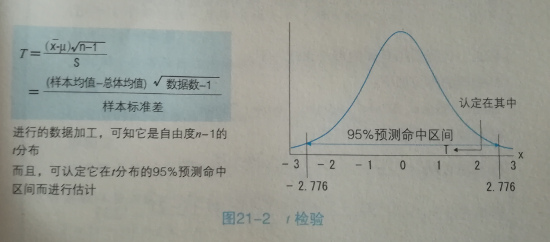
$T=(样本均值-总体均值)\div(样本标准差)\times \sqrt{n-1}$是服从自由度n-1的t分布
利用t分布估计正态母群体的总体均值的方法:
- 从所得的n个样本计算样本均值$\frac{}{x}$和样本标准差s。
- 使用样本均值$\frac{}{x}$、样本标准差s和想要估计的总体均值$\mu$,按照如下计算服从自由度n-1的t分布的统计量T。
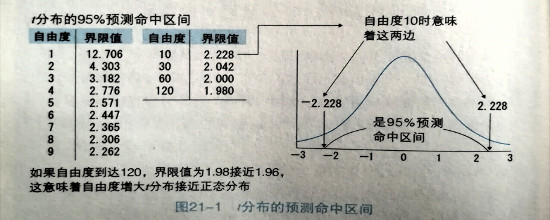
$$T=(\frac{}{x}-\mu)\div s\times\sqrt{n-1}$$ - 在图21-1查自由度n-1的95%预测命中区间,做$-\alpha\leq T\leq+\alpha$这样的预测区间。
- 解$-\alpha\leq\frac{(\frac{}{x}-\mu)\sqrt{n-1}}{s}\leq+\alpha$中的$\mu$,即为95%置信区间。
练习
某居酒屋的店主想进行营业额的预测。店主将营业额看作正态母群体中的观测数据,想要估计作为营业额代表的总体均值$\mu$。从发票中随机抽取8枚,出现了如下数字
45、39、42、57、28、33、40、52(单位为日元)。
按照以下的顺序对总体均值$\mu$进行区间估计:
首先,样本均值$\frac{}{x}=(42)$。其次计算样本方差。
$$s^2=\frac{9+9+0+225+196+81+4+100}{8}=78$$
因此,样本标准差s=(8.83)。
计算T
$$T=\frac{[(42)-\mu]\sqrt{(8)-1}}{8.83}=[(42)-\mu]\times (0.3)$$
T服从自由度(7)的t分布,所以可以求满足
$$(-2.365)\leq[(42)-\mu]\times (0.3)\leq(+2.365)的\mu$$
解得$$34.12\leq\mu\leq49.88$$