第十七章《用卡方分布推算总体方差——推算正态母群体的总体方差》。
总结
- 由一般正态母群体作卡方分布V的方法
从总体均值$\mu$、总体标准差$\sigma$的正态母群体中观测n个样本$x_1$、$x_2$、……$x_n$,计算$$V=(\frac{x_1-\mu}{\sigma})^2+(\frac{x_2-\mu}{\sigma})^2+…+(\frac{x_n-\mu}{\sigma})^2$$求V,得统计量V是自由度n的卡方分布。
- 从已知总体均值$\mu$的正态母群体中的n个数据估计总体方差$\sigma^2$的95%置信区间,可按照以下步骤:
- 由n个数据使用上述方法计算V。V是(数字/$\sigma^2$)的形式。
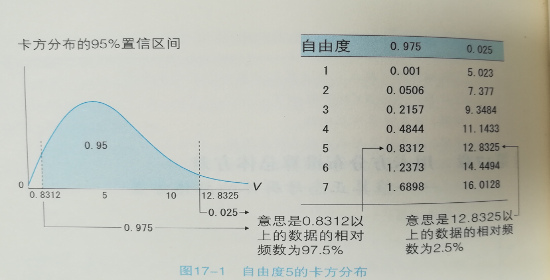
- 从图中可求自由度n的卡方分布的95%预测命中区间为a以上b以下的形式。
- 解不等式$a\leq\frac{数字}{\sigma^2}\leq b$,求$\sigma^2$。
练习
已知某蝴蝶体长的母群体为总体均值80mm的正态母群体。此时,观测到的4个个体的体长为76mm、77mm、83mm、84mm。总体方差为$\sigma^2$,求$\sigma^2$的95%置信区间(参照上图)。
首先,计算V。
$$V=(\frac{76-80}{\sigma})^2+(\frac{77-80}{\sigma})^2+(\frac{83-80}{\sigma})^2+(\frac{84-80}{\sigma})^2$$
$$V=\frac{50}{\sigma^2}$$
因为V呈自由度(4)的卡方分布,求满足$$(0.4844)\leq\frac{50}{\sigma^2}\leq(11.1433)$$的$\sigma^2$。解得95%的置信区间为$$(4.487)\leq\sigma^2\leq(103.22)$$