摘要
自由度。在统计学中,自由度(英语:degree of freedom, df)是指当以样本的统计量来估计总体的参数时,样本中独立或能自由变化的数据的个数,称为该统计量的自由度。一般来说,自由度等于独立变量减掉其衍生量数;举例来说,变异数的定义是样本减平均值(一个由样本决定的衍伸量),因此对N个随机样本而言,其自由度为N-1。
自由度n的卡方分布。从标准正态母群体中观测n个数据,平方相加做统计量V,V的分布为“自由度n的卡方分布”。这些分布根据自由度n变化形状。
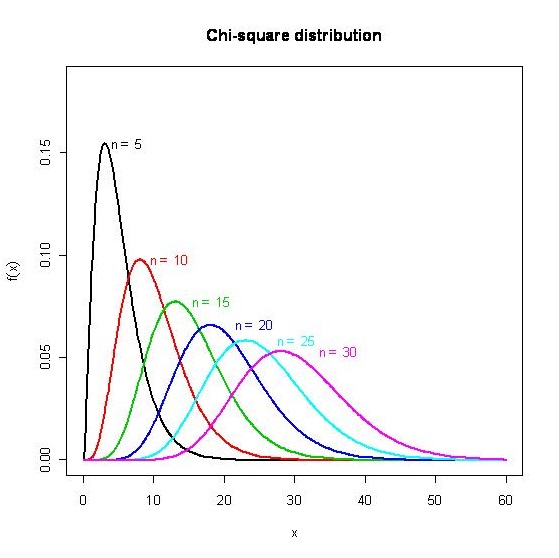
卡方分布的特征。
- 0的附近数据的相对频数大(就是说,直方图呈过山车形)。这是正态分布在0的附近数据的相对频数大的反映。
- 随着自由度n(观测数据数)的增大,山的高度渐渐向右侧变低(过山车的倾斜是平缓的)。这表明了n增大,稍稍远离0的数据出现的相对频数增高。
自由度3的卡方分布相对频数表:
| V | X以上出现的相对频数 |
|---|---|
| 0 | 1 |
| 1 | 0.8012 |
| 2 | 0.5724 |
| 3 | 0.3916 |
| 4 | 0.2614 |
| 5 | 0.1717 |
| 6 | 0.1116 |
| 7 | 0.0718 |
| 8 | 0.0460 |
| 9 | 0.0292 |
| 10 | 0.0185 |
如上图,数值X旁边写的数值,表示“X以上数据占全体多少比例”。4的地方是0.2614,这意味着4以上数值出现的相对频数约为0.2614,即自由度3的卡方分布的数据中4以上的占全体的大约26.14%。同理,10以上的数据出现的相对频数只有1.8%。这就可以确认卡方分布的数据是如何只在0的附近集中的。
总结
观测数据(样本)中计算的方差叫作“样本方差”。
计算样本方差 $s^2$ 的步骤如下:
- 步骤1 首先计算样本均值。
- 步骤2 其次从各样本中减去样本均值,作偏差。
- 步骤3 将各偏差进行平方再合计,除以样本数。
- 公式写作:
$$ (样本方差s^2) = \frac{[(偏差1)^2+(偏差2)^2+…+(偏差n)^2]}{n}$$
自由度n的卡方分布的V
对于标准正态分布母群体中n个样本$x_1$、$x_2$、…$x_n$,将它们平方再合计
$$V={x_1}^2 + {x_2}^2 + … + {x_n}^2$$
得统计量V,V呈自由度n的卡方分布。卡方分布的V,只出现0以上的值。另外,距0近的数值的相对频数大,距0远的数值的相对频数急剧减小。
练习
观测3次根据标准正态分布得到的数据。此时,利用上图,求观测到的3个数值的平方的和在2以上不到7的相对频数。
2以上的相对频数=(0.5724)
7以上的相对频数=(0.0718)
2以上不到7的相对频数=(0.5724)-(0.0718)=(0.5006)。