Fanzhh's Blog
0%

Machine Learning in Action Chapter 3

Posted on Edited on In

《机器学习实战》第三章决策树源码及分析。

源码

trees.py

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
#-*-coding:utf-8-*-

from math import log
import operator

def calcShannonEnt(dataSet):
    """
    计算给定数据集的香农熵
    """
    # 计算数据集中实例的总数
    numEntries = len(dataSet) 
    # 创建一个数据字典，其键值是数据集最后一列的数值
    labelCounts = {}
    for featVec in dataSet:
        currentLabel = featVec[-1]
        if currentLabel not in labelCounts.keys():
            labelCounts[currentLabel] = 0
        # 累计类标签出现的次数
        labelCounts[currentLabel] += 1
    shannonEnt = 0.0
    for key in labelCounts:
        # 计算香农熵
        prob = float(labelCounts[key])/numEntries
        shannonEnt -= prob * log(prob,2)
    return shannonEnt

def createDataSet():
    """
    创建测试数据集及标签
    """
    dataSet = [[1,1,'yes'],
            [1,1,'yes'],
            [1,0,'no'],
            [0,1,'no'],
            [0,1,'no']]
    labels = ['no surfacing', 'flippers']
    return dataSet, labels

def splitDataSet(dataSet,axis,value):
    """
    按照给定特征划分数据集，参数：
    dataSet: 待划分的数据集,
    axis: 划分数据集的特征,
    value: 需要返回的特征值
    """
    # 创建新的列表对象
    retDataSet = []
    for featVec in dataSet:
        # 将符合特征的数据抽取出来
        if featVec[axis] == value:
            reducedFeatVec = featVec[:axis]
            reducedFeatVec.extend(featVec[axis+1:])
            retDataSet.append(reducedFeatVec)
    return retDataSet

def chooseBestFeatureToSplit(dataSet):
    """
    该函数实现选取特征，划分数据集，计算得出最好的划分数据集的特征。
    函数中调用的数据需要满足的要求：
    1.数据必须是一种列表，且所有的列表元素都具有相同的数据长度；
    2.数据的最后一列（或每个实例的最后一个元素）是当前实例的类别标签。
    """
    numFeatures = len(dataSet[0]) - 1
    # 计算整个数据集的原始香农值
    baseEntropy = calcShannonEnt(dataSet)
    bestInfoGain = 0.0 
    bestFeature = -1
    for i in range(numFeatures):
        # 创建唯一的分类标签列表
        featList = [example[i] for example in dataSet]
        uniqueVals = set(featList)
        newEntropy = 0.0
        for value in uniqueVals:
            subDataSet = splitDataSet(dataSet,i,value)
            prob = len(subDataSet)/float(len(dataSet))
            newEntropy += prob * calcShannonEnt(subDataSet)
        infoGain = baseEntropy - newEntropy
        if (infoGain > bestInfoGain):
            bestInfoGain = infoGain
            bestFeature = i
    return bestFeature

def majorityCnt(classList):
    """
    使用分类名称的列表，创建键值为列表中唯一值的数据字典，
    字典对象储存每个类标签出现的频率，对字典排序，返回出
    现次数最多的分类名称。
    """
    classCount = {}
    for vote in classList:
        if vote not in classCount.keys():
            classCount[vote] = 0
        classCount[vote] += 1
        sortedClassCount = sorted(classCount.iteritems(),\
                key = operator.itemgetter(1), reverse=True)
        return sortedClassCount[0][0]

def createTree(dataSet,labels):
    """
    创建分类树。
    """
    # 创建包含数据集所有类标签的列表变量
    classList = [example[-1] for example in dataSet]
    # 列表中类别完全相同则停止继续划分，返回类别标签
    if classList.count(classList[0]) == len(classList):
        return classList[0]
    # 使用完了所有特征，仍然不能将数据集划分成仅包含唯一
    # 唯一类别的分组，返回出现次数最多的类别。
    if len(dataSet[0]) == 1:
        return majorityCnt(classList)
    # 选择划分数据集的最好特征
    bestFeat = chooseBestFeatureToSplit(dataSet)
    bestFeatLabel = labels[bestFeat]
    # myTree存储树的所有信息
    myTree = {bestFeatLabel:{}}
    del (labels[bestFeat])
    # 得到列表包含的所有属性值
    featValues = [example[bestFeat] for example in dataSet]
    uniqueVals = set(featValues)
    for value in uniqueVals:
        subLabels = labels[:]
        myTree[bestFeatLabel][value] = createTree(splitDataSet\
                (dataSet,bestFeat,value),subLabels)
    return myTree

def classify(inputTree,featLabels,testVec):
    """
    使用决策树的分类函数。
    """
    firstStr = inputTree.keys()[0]
    secondDict = inputTree[firstStr]
    # 查找当前列表中第一个匹配firstStr变量的元素
    featIndex = featLabels.index(firstStr)
    for key in secondDict.keys():
        if testVec[featIndex] == key:
            if type(secondDict[key]).__name__=='dict':
                classLabel = classify(secondDict[key],featLabels,testVec)
            else:
                classLabel = secondDict[key]
    return classLabel

def storeTree(inputTree,filename):
    """
    使用pickle模块存储决策树
    """
    import pickle
    fw = open(filename,'w')
    pickle.dump(inputTree,fw)
    fw.close()

def grabTree(filename):
    import pickle
    fr = open(filename)
    return pickle.load(fr)

treePlotter.py

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
#-*-coding:utf-8-*-
import matplotlib.pyplot as plt

decisionNode = dict(boxstyle="sawtooth",fc="0.8")
leafNode = dict(boxstyle="round4", fc="0.8")
arrow_args = dict(arrowstyle="<-")

def plotNode(nodeTxt, centerPt, parentPt, nodeType):
    createPlot.ax1.annotate(nodeTxt,xy=parentPt,\
            xycoords='axes fraction',\
            xytext=centerPt, textcoords='axes fraction',\
            va="center", ha="center",bbox=nodeType,arrowprops=arrow_args)

def createPlot():
    fig = plt.figure(1,facecolor='white')
    fig.clf()
    createPlot.ax1 = plt.subplot(111,frameon=False)
    plotNode(u'决策节点',(0.5,0.1),(0.1,0.5),decisionNode)
    plotNode(u'叶节点',(0.8,0.1),(0.3,0.8),leafNode)
    plt.show()

def getNumLeafs(myTree):
    numLeafs = 0
    firstStr = myTree.keys()[0]
    secondDict = myTree[firstStr]
    for key in secondDict.keys():
        if type(secondDict[key]).__name__=='dict':
            numLeafs += getNumLeafs(secondDict[key])
        else:
            numLeafs += 1
    return numLeafs

def getTreeDepth(myTree):
    maxDepth = 0
    firstStr = myTree.keys()[0]
    secondDict = myTree[firstStr]
    for key in secondDict.keys():
        if type(secondDict[key]).__name__=='dict':
            thisDepth = 1+ getTreeDepth(secondDict[key])
        else:
            thisDepth = 1
        if thisDepth > maxDepth:
            maxDepth = thisDepth
    return maxDepth

def retrieveTree(i):
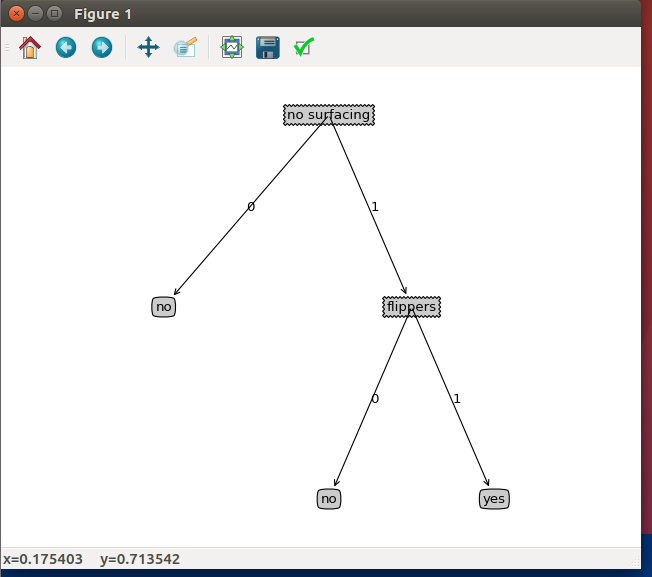
    listOfTrees = [{'no surfacing':{0:'no',1:{'flippers':\
            {0:'no',1:'yes'}}}},
            {'no surfacing':{0:'no',1:{'flippers':\
                    {0:{'head':{0:'no',1:'yes'}},1:'no'}}}}]
    return listOfTrees[i]
    
def plotMidText(cntrPt,parentPt,txtString):
    xMid = (parentPt[0]-cntrPt[0])/2.0 + cntrPt[0]
    yMid = (parentPt[1]-cntrPt[1])/2.0 + cntrPt[1]
    createPlot.ax1.text(xMid,yMid,txtString)
    
def plotTree(myTree,parentPt,nodeTxt):
    numLeafs = getNumLeafs(myTree)
    depth = getTreeDepth(myTree)
    firstStr = myTree.keys()[0]
    cntrPt = (plotTree.xOff + (1.0+float(numLeafs))/2.0/plotTree.totalW,\
            plotTree.yOff)
    plotMidText(cntrPt,parentPt,nodeTxt)
    plotNode(firstStr,cntrPt,parentPt,decisionNode)
    secondDict = myTree[firstStr]
    plotTree.yOff = plotTree.yOff - 1.0/plotTree.totalD
    for key in secondDict.keys():
        if type(secondDict[key]).__name__=='dict':
            plotTree(secondDict[key],cntrPt,str(key))
        else:
            plotTree.xOff = plotTree.xOff + 1.0/plotTree.totalW
            plotNode(secondDict[key],(plotTree.xOff,plotTree.yOff),\
                    cntrPt,leafNode)
            plotMidText((plotTree.xOff,plotTree.yOff),cntrPt,str(key))
    plotTree.yOff = plotTree.yOff + 1.0/plotTree.totalD

def createPlot(inTree):
    fig = plt.figure(1,facecolor='white')
    fig.clf()
    axprops = dict(xticks=[], yticks=[])
    createPlot.ax1 = plt.subplot(111,frameon=False,**axprops)
    plotTree.totalW = float(getNumLeafs(inTree))
    plotTree.totalD = float(getTreeDepth(inTree))
    plotTree.xOff = -0.5/plotTree.totalW
    plotTree.yOff = 1.0
    plotTree(inTree,(0.5,1.0),'')
    plt.show()

树形图

两个分支的树形图

由ID3算法产生的决策树

总结

决策树分类器就像带有终止块的流程图，终止块表示分类结果。开始处理数据时，首先要测量集合中数据的不一致性，也就是熵（熵的计算公式：$$ H=-\sum_{i=1}^np(x_i)log_2p(x_i) $$），然后寻找最优方案划分数据集，知道数据集中所有数据属于同一分类。