Machine Learning in Action Chapter 5

《机器学习实战》第五章Logistic回归的学习笔记及代码。

Logistic回归的一般过程

收集数据：采用任意方法收集数据。
准备数据：由于需要进行距离运算，因此要求数据类型为数值型。另外，结构化数据格式最佳。
分析数据：采用任意方法对数据进行分析。
训练算法：大部分时间将用于训练，目的是为了找到最佳的分类回归系数。
测试算法：一旦训练步骤完成，分类将会很快。
使用算法：首先，输入一些数据，并将其转换成对应的结构化数值；接着，基于训练好的回归系数就可以对这些数值进行简单的回归计算，判定他们属于哪个类别；最后，在输出的类别上做一些其他分析工作。

基于Logistic回归和Sigmoid函数的分类

Logistic回归的特点：

优点：计算代价不高，易于理解和实现。
缺点：容易欠拟合，分类精度可能不高。
适用数据类型：数值型和标称型数据。

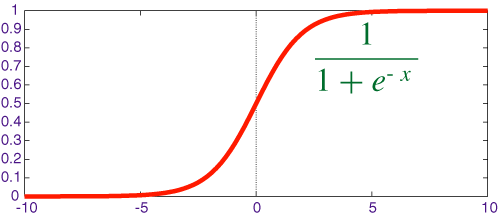
Sigmoid函数

Sigmoid函数是一种阶跃函数(step function)。在数学中，如果实数域上的某个函数可以用半开区间上的指示函数的有限次线性组合来表示，那么这个函数就是阶跃函数。

Sigmoid函数的计算公式：

$$ỽ(z)=\frac{1}{1+e^{-z}}$$

基于最优化方法的最佳回归系数确定

Sigmoid函数的输入为z，由下面公式得出：
$$z=w_0x_0+w_1x_1+w_2x_2+…+w_nx_n$$

采用向量写法，上述公式可以写成：
$$z=w^Tx$$

其中向量x是分类器的输入数据，w是我们要找到的最佳参数（系数），从而使分类器尽可能准确。

梯度上升法

梯度上升法的迭代公式：
$$w:=w+aⱯ_wf(w)$$

训练算法：使用梯度上升找到最佳参数

梯度上升法的伪代码：

每个回归系数初始化为1
重复R次：
	计算整个数据集的梯度
	使用alpha x gradient更新回归系数的向量
	返回回归系数

程序清单：Logistic回归梯度上升优化算法

from numpy import mat,shape,ones,exp

def loadDataset():
    dataMat = []; labelMat = []
    fr = open('chapter_5/testSet.txt')
    for line in fr.readlines():
        lineArr = line.strip().split()
        dataMat.append([1.0,float(lineArr[0]),float(lineArr[1])])
        labelMat.append(int(lineArr[2]))
    return dataMat,labelMat

def sigmoid(inX):
    return 1.0/(1+exp(-inX))

def gradAscent(dataMatIn,classLabels):
    dataMatrix = mat(dataMatIn)
    labelMat = mat(classLabels).transpose()
    m,n = shape(dataMatrix)
    alpha = 0.001
    maxCycles = 500
    weights = ones((n,1))
    for k in range(maxCycles):
        h = sigmoid(dataMatrix*weights)
        error = (labelMat-h)
        weights = weights + alpha*dataMatrix.transpose()*error
    return weights

在python提示符下，输入以下代码：

import logRegres
dataArr,labelMat = logRegres.loadDataSet()
logRegres.gradAscent(dataArr,labelMat)
...

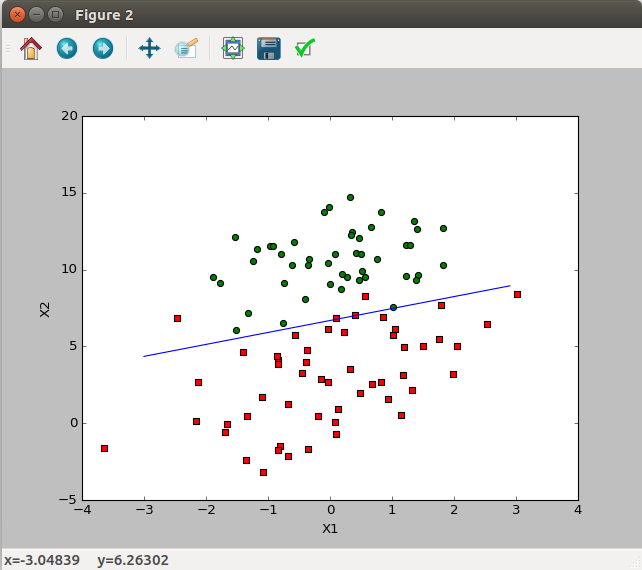
分析数据：画出决策边界

def plotBestFit(weights):
    import matplotlib.pyplot as plt
    dataMat,labelMat = loadDataset()
    dataArr = array(dataMat)
    n = shape(dataArr)[0]
    xcord1 = []; ycord1 = []
    xcord2 = []; ycord2 = []
    for i in range(n):
        if int(labelMat[i]) == 1:
            xcord1.append(dataArr[i,1]); ycord1.append(dataArr[i,2])
        else:
            xcord2.append(dataArr[i,1]); ycord2.append(dataArr[i,2])
    fig = plt.figure()
    ax = fig.add_subplot(111)
    ax.scatter(xcord1,ycord1,s=30,c='red',marker='s')
    ax.scatter(xcord2,ycord2,s=30,c='green')
    x = arange(-3.0,3.0,0.1)
    # 此处设置figmoid函数为0,0是两个分类的分界处，因此设定
    # 0=w0x0+w1x1+w2x2，然后解出X2和X1的关系式（即分割线的方程，注意X0=1)。
    y = (-weights[0]-weights[1]*x)/weights[2]
    ax.plot(x,y)
    plt.xlabel('X1'); plt.ylabel('X2');
    plt.show()

训练算法：随机梯度上升

梯度上升算法在每次更新回归系数时都要遍历整个数据集，如果样本数量大，该方法的计算复杂度就太高了。一种改进方法是一次仅用一个样本点来更新回归系数，该方法称为随机梯度上升算法。由于可以在新样本到来时对分类器进行增量式更新，因而随机梯度上升算法是一个在线学习算法。与“在线学习”相对应，一次处理所有数据被称作是“批处理”。

随机梯度算法可以写成以下伪代码：

所有回归系数初始化为1
对数据集中每个样本
    计算该样本的梯度
    使用 alpha x gradient 更新回归系数值
返回回归系数值

以下为实现代码：

def stocGradAscent0(dataMatrix,classLabels):
    m,n = shape(dataMatrix)
    alpha = 0.01
    weights = ones(n)
    for i in range(m):
        h = sigmoid(sum(dataMatrix[i]*weights))
        error = classLabels[i] - h
        weights = weights + alpha*error*dataMatrix[i]
    return weights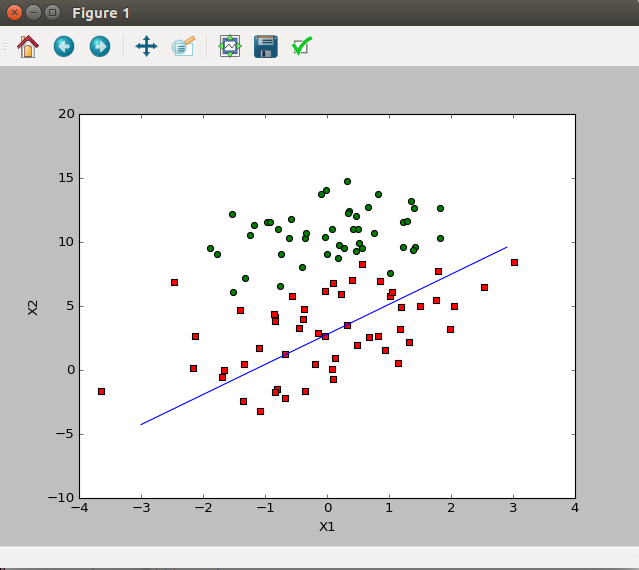

对上述算法进行修改，使其在整个数据集上运行200次：

改进后的随机梯度上升算法：

def stocGradAscent1(dataMatrix,classLabels,numIter=150):
    m,n = shape(dataMatrix)
    weights = ones(n)
    for j in range(numIter):
        dataIndex = range(m)    
        for i in range(m):
            # alpha在每次迭代的时候都会调整，这会缓解数据波动或高频波动。
            # 虽然alpha会随着迭代次数不断减小，但永远不会减小到0.
            # 必须这样做的原因是为了保证在多次迭代之后新数据仍然具有一定影响。
            alpha = 4/(1.0+j+i)+0.01
            # 这里通过随机选取样本来更新回归系数。这种方法将较少周期波动。
            randIndex = int(random.uniform(0,len(dataIndex)))
            h = sigmoid(sum(dataMatrix[randIndex]*weights))
            error = classLabels[randIndex] - h
            weights = weights + alpha*error*dataMatrix[randIndex]
            del(dataIndex[randIndex])
    return weights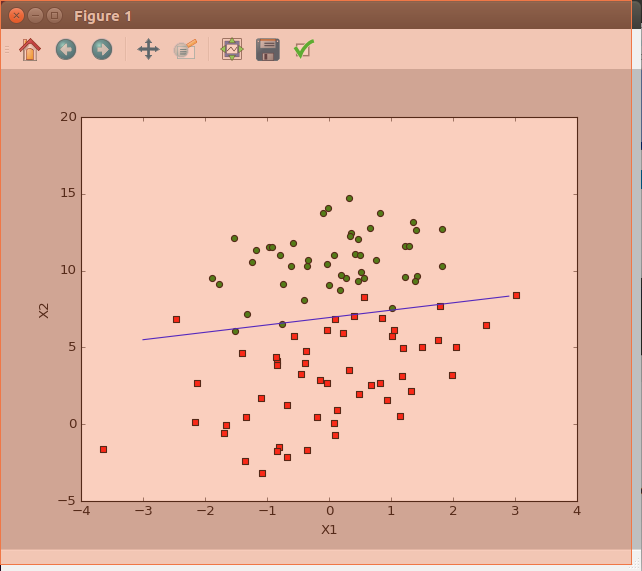

示例：从疝气病症预测病马的死亡率

收集数据：给定数据文件。
准备数据：用Python解析文本文件并填充缺失值。
分析数据：可视化并观察数据。
训练算法：使用优化算法，找到最佳系数。
测试算法：为了量化回归的效果，需要观察错误率。根据错误率决定是否回退到训练阶段，通过改变迭代的次数和步长等参数来得到更好的回归系数。
使用算法。

准备数据：处理数据中的缺失值

一些处理数据中的缺失值的可选做法：

使用可用特征的均值来填补缺失值；
使用特殊值来填补缺失值，如-1;
忽略有缺失的样本；
使用相似样本的均值添补缺失值；
使用另外的机器学习算法预测缺失值。

测试算法：用Logistic回归进行分类

def classifyVector(inX,weights):
    prob = sigmoid(sum(inX*weights))
    if prob>0.5:
        return 1.0
    else:
        return 0.0

def colicTest():
    frTrain = open('chapter_5/horseColicTraining.txt')
    frTest = open('chapter_5/horseColicTest.txt')
    trainingSet = []; trainingLabels = []
    for line in frTrain.readlines():
        currLine = line.strip().split('\t')
        lineArr = []
        for i in range(21):
            lineArr.append(float(currLine[i]))
        trainingSet.append(lineArr)
        trainingLabels.append(float(currLine[21]))
    trainWeights = stocGradAscent1(array(trainingSet),trainingLabels,500)
    errorCount = 0; numTestVec = 0.0
    for line in frTest.readlines():
        numTestVec += 1.0
        currLine = line.strip().split('\t')
        lineArr = []
        for i in range(21):
            lineArr.append(float(currLine[i]))
        if int(classifyVector(array(lineArr),trainWeights))!=int(currLine[21]):
            errorCount += 1
    errorRate = (float(errorCount)/numTestVec)
    print "the error rate of this test is: %f" % errorRate
    return errorRate

def multiTest():
    numTests = 10; errorSum = 0.0
    for k in range(numTests):
        errorSum += colicTest()
    print "after %d iterations the average error rate is: %f" % (numTests,errorSum/float(numTests))

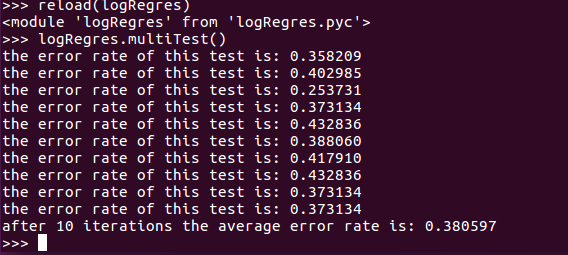
小结

Logistic回归的目的是寻找一個非线性函数Sigmoid的最佳拟合参数，求解过程可以由最优化算法来完成。在最优化算法中，最常用的就是梯度上升算法，而梯度上升算法又可以简化为随机梯度上升算法。

随机梯度上升算法与梯度上升算法的效果相当，但占用更少的系统资源。此外，随机梯度上升算法是一个在线算法，可以在新数据到来时就完成参数更新，而不需要重新读取整个数据集来进行批处理运算。